by Ben Evans, CFD Engineer & Aerodynamicist – BLOODHOUND aerodynamics
Most engineering fluid flow problems are now solved, at least in part, by using computational fluid dynamics (CFD). What this means is that we can use computers to help us solve the equations that govern fluid dynamics, rather than having to do them by hand.
Which equations matter?
The governing equations for the majority of practical fluid flow problems are partial differential equations (PDEs) – in fact, that's the case for many naturally occurring phenomena. If you studied (or are studying) mathematics at A-level, you will probably have come across some simple differential equations and solved them analytically (using pen and paper).
The set of equations that are most relevant for describing the aerodynamic flows around BLOODHOUND are the so-called ‘Navier-Stokes’ equations. These are a set of five PDEs describing quantities such as the density, velocity and pressure of the airflow. (There's also a sixth equation if you want to model turbulence in the flowfield).
To get some idea of the degree of complexity of this set of equations, have a look at figure 1.

Figure 1: The Navier-Stokes equations for viscous, compressible fluid flow
There is no hope of solving such a complex and coupled set of equations such as this by hand – even large supercomputers have to work hard to obtain solutions!
The challenge in CFD
The development of CFD techniques has closely followed the development of numerical methods for solving partial differential equations. Numerical methods have been known since the time of Newton in the 1700s, but without the aid of the computer it was impossible to fully exploit these techniques.
Modern CFD has its roots in the 1950s with the advent of the digital computer. At the heart of all CFD numerical schemes is the fundamental question of how to represent a continuous function at a finite set of points (we call this 'discretisation'). In other words, how can we store a function defined for an infinite number of points (i.e. every possible position in space and time) in a finite way, and as accurately as possible?
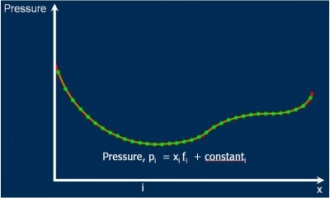 Figure 2: Example of the discretisation / approximation of a pressure function
Figure 2: Example of the discretisation / approximation of a pressure function
Here's an example. In figure 2 a pressure function has been 'discretised' so that the value of the function at a finite number of ‘nodes’ is stored and a linear interpolation of the solution is assumed between the nodes. The jump between each node is referred to as an 'element' and hence this kind of solution is often referred to as ‘the finite element method’.
3D solutions
The most popular method of achieving a three-dimensional finite element solution is to discretise the solution domain into a finite number of small cells or elements forming a mesh or grid, and to then apply a suitable algorithm to values stored at the intersections of the mesh (the nodes) to solve the governing equations – in our case, the Navier-Stokes equations.
The computational mesh can consist of elements of a whole variety of 3D shapes. For the CFD work carried out on BLOODHOUND, a mesh of hexahedra, prisms and tetrahedra numbering into the tens of millions was used!
CFD and BLOODHOUND
The procedure for performing the CFD analysis on BLOODHOUND can best be described in the following stages:
1. The definition of the vehicle surface to be examined was provided to the team at Swansea University as a CAD (computer-aided-design) output from the design engineers based in the design office in Bristol. This geometry definition was then analysed via the FLITE3D computer system developed at the College of Engineering at Swansea University.
2. The CAD output was processed and a mesh generation computer program used to construct the computational mesh.
3. A ‘pre-processing’ computer program was then used to format the mesh in such a way that the Swansea University supercomputing cluster could be used to run the solver program. Over the course of the BLOODHOUND project we have also had computational support in the form of access to large supercomputers from Intel and HPC Wales.
4. The ‘equation solver’ program containing the Navier-Stokes solution algorithm was run on the supercomputing cluster.
5. A ‘post-processing’ software package was used to convert the solutions coming from the solver into meaningful flow visualisation plots and force distributions.
A selection of outputs from final visualisation stage is shown in figures 3 and 4. These visualisations helped the design team understand the behaviour of the car’s aerodynamics in terms of flow phenomena such as shock waves, boundary layers (the thin layer of slow-moving air close to the Car's surface) and pressure distributions. These pictures and force distributions were analysed and changes made to the design, and we then repeated steps 1 to 5 to check the outcomes of those changes.
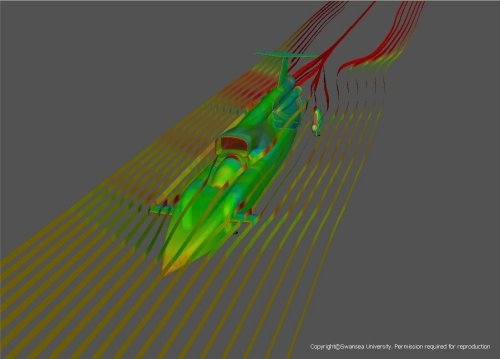
Figure 3: Streamribbons and pressure contours over an intermediate BLOODHOUND configuration
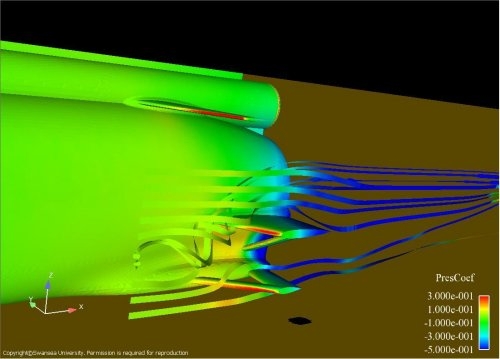
Figure 4: Visualisation of a vortex being shed at the rear of BLOODHOUND impinging on the rear wheel struts
Where else can we use CFD?
The applications for the computational modelling technologies being developed at Swansea are wide ranging, including: medicine; lightning strike modelling; building structural analysis; and even interstellar plasma flows. Essentially, any phenomena governed by partial differential equations can be simulated using the computational modelling approach of the finite element method.
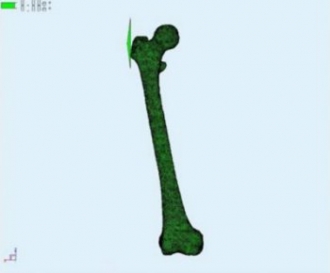
In figure 6 you can see how biomedical modelling of stresses in a human femur is a phenomenon that can be described by a set of partial differential equations that can be modelled using the same techniques of finite elements that we used to study the aerodynamics of BLOODHOUND SSC.
Figures 5 and 6: Fluid-structure interaction modelling of a typical jet airliner; biomedical modelling of stresses in a human femur

Swansea University

Swansea University is proud to be part of the BLOODHOUND team. Our work on computer fluid dynamics (CFD) is at the heart of research on the design and aerodynamics of the 1,000mph Car.
Swansea University is a world-class research-led dual campus university. Its main base, Singleton Park Campus, is located on a beautiful 47 acre parkland estate and its £450 million Bay Campus, which opened to students in September 2015, is based on the beach on the eastern side of Swansea city centre.
The University was established in 1920 and currently offers around 350 undergraduate courses and 100 post-graduate courses to over 19,000 undergraduate and postgraduate students.
 Ben Evans showcases a model of the BLOODHOUND SSC to school children at the launch in 2008 at the National Waterfront Museum
Ben Evans showcases a model of the BLOODHOUND SSC to school children at the launch in 2008 at the National Waterfront Museum
Swansea University continues to maintain its position as one of the top universities in the UK for engineering. The College of Engineering is now based at Swansea University’s Bay Campus , which has four buildings dedicated to engineering, holding 30,000m2 of laboratory and office space and over £10 million of new research and teaching equipment.
The College of Engineering is ranked within the Top 10* in the UK and is internationally recognised for its cutting-edge research with 94% of research produced by academic staff rated World-Leading or Internationally Excellent quality** .

The College has strong and establish links with a large variety of local, national and international companies both with its teaching and research. It has significantly contributed to a number of prestigious projects from the aerodynamics design of the THRUST Supersonic Car, which currently holds the World Land Speed Record, to BLOODHOUND.
The computer fluid dynamics (CFD) research for BLOODHOUND is being undertaken at the Zienkiewicz Centre for Computational Engineering (ZCCE) one of four research centres with the College.
To find out more about the College of Engineering please go to our website www.swansea.ac.uk/engineering or follow us on Facebook, Twitter or Instagram .
* The Times & Sunday Times University Guide 2016
** Research Excellent Framework 2014


